GPU621/Threadless Horsemen
Contents
Comparing Multi-threading in Julia vs OpenMP
Group Members
Introduction: The Julia Programming Language
Bit of History
- It's a relatively new language and runtime (started in 2009, launched in 2012).
- The 1.0 release happened this August (https://julialang.org/blog/2018/08/one-point-zero)
- It's very ambitious in the sense that it aims to be very good in several areas.
- It was originally thought up by Stefan Karpinski, a CS grad student working on simulating wireless networks
" STEFAN KARPINSKI WAS building a software tool that could simulate the behavior of wireless networks, and his code was a complete mess. But it wasn't his fault. ... He knew how to build software. The problem was that in order to build his network simulation tool, he needed four different programming languages. No single language was suited to the task at hand, but using four languages complicated everything from writing the code to debugging it and patching it. ... Today's languages were each designed with different goals in mind. Matlab was built for matrix calculations, and it's great at linear algebra. The R language is meant for statistics. Ruby and Python are good general purpose languages, beloved by web developers because they make coding faster and easier. But they don't run as quickly as languages like C and Java. What we need, Karpinski realized after struggling to build his network simulation tool, is a single language that does everything well." https://www.wired.com/2014/02/julia/
More info: Developers' blog post on why they created Julia: https://julialang.org/blog/2012/02/why-we-created-julia
Takeaway
- MATLAB is often used for matrix calculations and linear algebra
- R is used for statistical computing
- Python is used for data science, scripting, web development
- They might provide great libraries and developer efficiency due to language design, but they're slower than C.
Julia has syntax which resembles python, and is JIT compiled to native machine code thanks to LLVM (Low-level Virtual Machine). It aims to provide great developer efficiency as well as fast execution times. Amongst the Julia community, the language is sometimes referred to as a potential MATLAB killer. It's open source, and the programs execute faster while keeping syntax simple.
Use Cases
Various organizations have used Julia in their projects, in a variety of fields (Machine Leaning, Bioinformatics, Astronomy, Insurance, Energy, Robtics, etc).
Small Excerpt from Racefox (digital sports coaching company):
"Racefox’s classification and motion analysis algorithms were first implemented in C++ to ensure fast execution. Initially, the team planned to send raw accelerometer data from the mobile device to the cloud for processing. ... Modifying the existing C++ code was proving too slow owing to the brittleness of the language, verbosity, and the need to go through lengthy modify-compile-run cycles. Racefox’s initial attempt to reimplement their algorithms in Matlab did not work very well. It involved a great deal of signal processing with for-loops and conditionals, something that Matlab was particularly bad at. The whole modify-run-analyze cycle was incredibly slow on Matlab, limiting the scope of experimentation. ... In about a week, they had a Julia implementation up and running that was orders of magnitude faster than their Matlab implementation. This was back in the Julia 0.2 days. Even as a young language, Julia was proving indispensable. Racefox was able to (very happily) abandon their C++ implementation and focus on one code base for both experimentation and production." https://juliacomputing.com/case-studies/racefox.html
More Use Cases: https://juliacomputing.com/case-studies/
- Julia computing was co-founded by the co-creators of Julia to provide support, consulting and other services to organizations using Julia
- The company raised $4.6M in seed funding last year (http://www.finsmes.com/2017/06/julia-computing-raises-4-6m-in-seed-funding.html)
Julia's Forms of Parallelism
Multi-threading
- Experimental in Julia
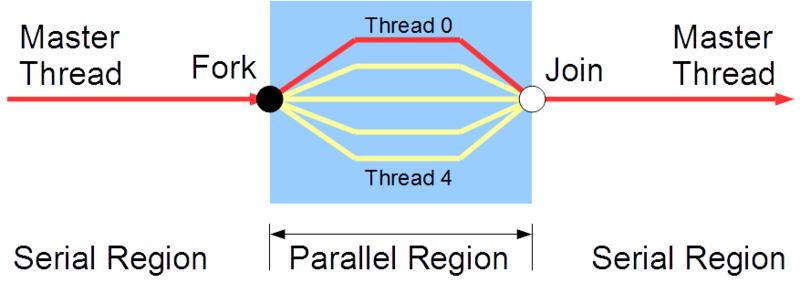
- Implements the fork join pattern (we've done it many times now)
- We focused on this in our quantitative testing, since at the time of writing code, we only had experience with OpenMP
Multi-core Or Distributed Processing
"Most modern computers possess more than one CPU, and several computers can be combined together in a cluster. ... Julia provides a multiprocessing environment based on message passing to allow programs to run on multiple processes in separate memory domains at once." https://docs.julialang.org/en/v1/manual/parallel-computing/
- Implements message passing
- Similar to MPI, but has some key differences
Message passing in Julia is one sided (programmer only explicitly manages one process in a two-process op).
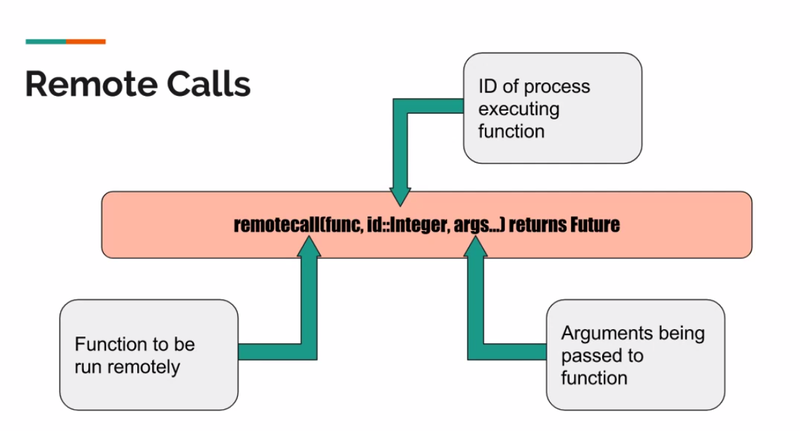
"Distributed programming in Julia is built on two primitives: remote references and remote calls. A remote reference is an object that can be used from any process to refer to an object stored on a particular process. A remote call is a request by one process to call a certain function on certain arguments on another (possibly the same) process." https://docs.julialang.org/en/v1/manual/parallel-computing/
Unlike sending and receiving messages using MPI, in Julia you would invoke a remote call, which is async.
- you pass in the function, id of process to execute it, and args for the function
- a Future is returned, which is a remote reference to the memory location associated with the process executing the function
- you can call fetch on the Future to get the result
https://www.youtube.com/watch?v=RlogUNQTf-M (Introduction to Julia and its Parallel Implmentation, 2:00)
# Example
# @everywhere lets all processes be able to call the function
@everywhere function whoami()
println(myid(), gethostname())
end
remotecall_fetch(whoami, 2)
remotecall_fetch(whoami, 4)
# remotecall_fetch is the same as fetch(remotecall(...))Source: https://www.dursi.ca/post/julia-vs-chapel.html#parallel-primitives
Coroutines (Green Threads)
Background:
- OS processes are instances of a program being executed, and each one has its own address space
- OS Threads are essentially lightweight processes, which share a process' address but maintain their own stack (processes can have many threads)
- Fibers are a newer concept, and they're essentially lightweight threads which have their own stacks and start/yield (stop) during thread execution (threads can have many fibers)
- Coroutines and fibers are functionally equivalent
"Fibers implement user space co-operative multitasking, rather than kernel level pre-emptive one. Thus, a fiber can not be forcefully pre-empted by the OS kernel ... Fibers do have their own stacks, but the fiber switching is done in user space by the execution environment, not the OS kernel generic scheduler. ... Fibers are a concurrency concept, but are not truly parallel. Typically, each fiber has a parent thread, just as each thread belongs to a process. Multiple fibers from the same thread can not run simultaneously. In other words, multiple execution paths can coexists in the form of fibers (i.e. concurrency) but they can not actually run at the same time (parallelism). ... Using a fiber library can be cumbersome, and thus some programming languages introduce coroutines. The two concepts are functionally equivalent. However, coroutines are implemented with specific syntax on the programming language level." https://nikgrozev.com/2015/07/14/overview-of-modern-concurrency-and-parallelism-concepts/
OpenMP vs Julia Code
For Multi-threading
- Need to install Julia runtime, and set JULIA_NUM_THREADS env var just like you set OMP_NUM_THREADS
- Julia code is more concise than C/C++ (also simpler to initialize arrays, don't need to manage memory)
- Note that OpenMp code uses loop interchange (ikj) and Julia doesn't (ijk), which will be explained in the next section
| OpenMP | Julia Multi-threading |
|---|---|
#include <omp.h>
#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <chrono>
#pragma once
#define N 512
typedef double array[N];
// matmul returns the product c = a * b
//
void matmul(const double a[][N], const double b[][N], double c[][N], int n) {
#pragma omp parallel for
for (int i = 0; i < n; i++) {
for (int k = 0; k < n; k++) {
for (int j = 0; j < n; j++) {
c[i][j] += a[i][k] * b[k][j];
}
}
}
}
// checksum returns the sum of the coefficients in matrix x[N][N]
//
double checksum(const double x[][N]) {
double sum = 0.0;
#pragma omp parallel for
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
sum += x[i][j];
}
}
return sum;
}
// initialize initializes matrix a[N][N]
//
void initialize(double a[][N]) {
#pragma omp parallel for
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
a[i][j] = static_cast<double>(i * j) / (N * N);
}
}
}
void reportTime(const char* msg, std::chrono::steady_clock::duration span) {
auto ms = std::chrono::duration_cast<std::chrono::milliseconds>(span);
std::cout << msg << ": " <<
ms.count() << " milliseconds" << std::endl;
}
int main(int argc, char** argv) {
if (argc != 1) {
std::cerr << "*** Incorrect number of arguments ***\n";
std::cerr << "Usage: " << argv[0] << "\n";
return 1;
}
std::cout << std::fixed << std::setprecision(2);
// allocate memory for matrices
double* a = new double[N*N];
double* b = new double[N*N];
double* c = new double[N*N];
array* aa = (array*)a;
array* bb = (array*)b;
array* cc = (array*)c;
std::cout << "Matrix Multiplication " << N << " by " << N << std::endl;
// initialize a and b
std::chrono::steady_clock::time_point ts, te;
ts = std::chrono::steady_clock::now();
initialize(aa);
initialize(bb);
double* t = c;
for (int i = 0; i < N * N; i++)
*t++ = 0.0;
te = std::chrono::steady_clock::now();
reportTime("initialization", te - ts);
// multiply matrices a and b
ts = std::chrono::steady_clock::now();
matmul(aa, bb, cc, N);
te = std::chrono::steady_clock::now();
reportTime("execution", te - ts);
std::cout << "checksum = " << checksum(cc) << std::endl;
// deallocate memory
delete[] a;
delete[] b;
delete[] c;
std::cout << "max threads: " << omp_get_max_threads() << std::endl;
} |
N = 512
function matmul(a, b, c, n)
Threads.@threads for i = 1:n
for j = 1:n
for k = 1:n
c[i,j] += a[i,k] * b[k,j]
end
end
end
return c
end
function checksum(x)
sum = 0.0
Threads.@threads for i = 1:N
for j = 1:N
sum += x[i,j]
end
end
return sum
end
# creates and returns 2d array of zeroes
function initialize()
a = zeros(Float64, N, N)
Threads.@threads for i = 1:N
for j = 1:N
a[i,j] = (convert(Float64,((i-1) * (j-1))) / convert(Float64, (N * N)))
end
end
return a
end
a = initialize();
b = initialize();
c = initialize();
start_t = time()
d = matmul(a, b, c, N)
end_t = time()
run_time = end_t - start_t
sum = checksum(d)
println("checksum = $sum")
println("matmul func time (s):")
println(run_time)
println("num threads: ")
nt = Threads.nthreads()
println(nt) |
More code here: https://github.com/tsarkarsc/parallel_prog
- If you don't care about using Threads, Julia has some features called macros which look similar to OpenMP's parallel constructs
- OpenMP of course uses multi-threading, whereas Julia uses Tasks, which is what they call their coroutines / fibers
- The following is a comparison of parallel reduction in OpenMP and Julia
| OpenMP | Julia |
|---|---|
template <typename T>
T reduce(
const T* in, // points to the data set
int n, // number of elements in the data set
T identity // initial value
) {
T accum = identity;
#pragma omp parallel for reduction(+:accum)
for (int i = 0; i < n; i++)
accum += in[i];
return accum;
} |
a = randn(1000)
@distributed (+) for i = 1:100000
some_func(a[rand(1:end)])
end |
- Note: Looks like Julia used to have a macro called @parallel so you could use, say, @parallel for, but it seems like it was deprecated in favour of @distributed
https://scs.senecac.on.ca/~gpu621/pages/content/omp_3.html
https://docs.julialang.org/en/v1/stdlib/Distributed/#Distributed.@distributed
https://docs.julialang.org/en/v1/manual/parallel-computing/index.html
https://github.com/JuliaLang/julia/issues/19578
OpenMP vs Julia Results
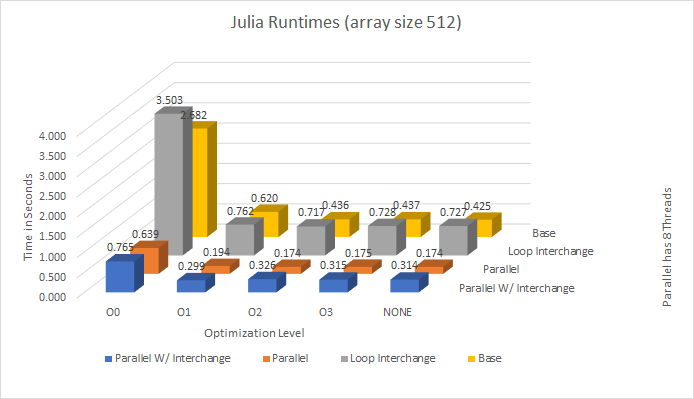
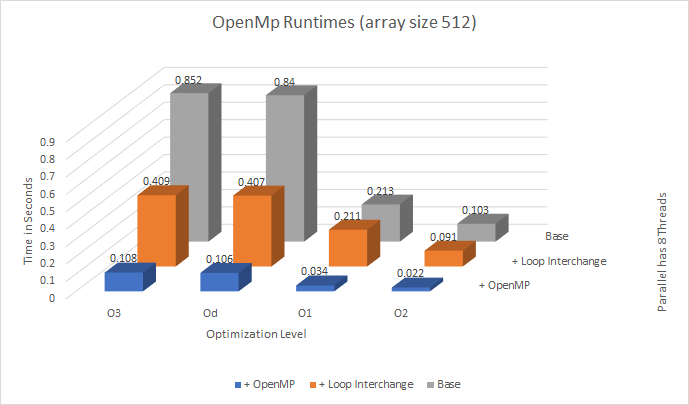
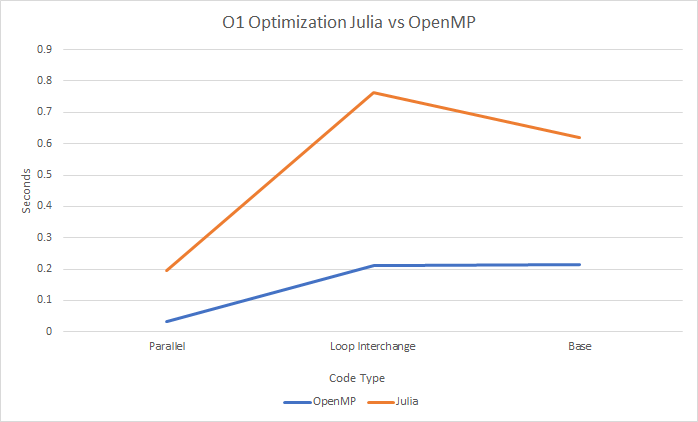
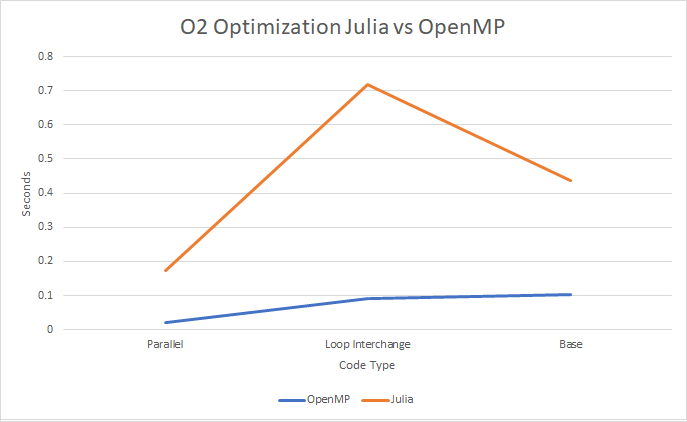
- We are taking the Workshop 3 as our test example and we are looking at the differences in speeds
- We decreased the size of the array to 512
- From here we wrote code for Julia to match the base, loop interchange and threading tests
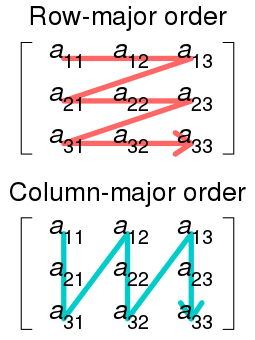
- The reason loop interchange works for OpenMP is the way we store our array in memory originally favored "Row-Major" which allows the processor to move across cached data in a row fashion faster than column based.
- As you might have seen, Julia’s loop interchange is worse it's for opposite reason OpenMP improves from loop interchange.
- Julia favours "Column-Major" layouts in cache memory.
- Julia has several levels of runtime optimization (0-3)
- julia -O2 scriptName.jl or julia --optimize=2
- Set the optimization level (default level is 2 if unspecified or 3 if used without a level -O)
Vectorization
- We want to briefly touch on vectorization
| Using Vectorization | Expanded axpy function |
|---|---|
function axpy(a,x,y)
@simd for i=1:length(x)
@inbounds y[i] += a*x[i]
end
end
n = 1003
x = rand(Float32,n)
y = rand(Float32,n)
axpy(1.414f0, x, y) |
function axpy(a::Float32, x::Array{Float32,1}, y::Array{Float32,1})
n=length(x)
i = 1
@inbounds while i<=n
t1 = x[i]
t2 = y[i]
t3 = a*t1[i]
t4 = t2+t3
y[i] = t4
i += 1
end
end |
- The @simd macro gives the compiler license to vectorize without checking whether it will change the program's visible behavior.
- The vectorized code will behave as if the code were written to operate on chunks of the arrays.
- @inbounds turns off subscript checking that might throw an exception.
- Make sure your subscripts are in bounds before using it or you might corrupt your Julia session.
More info on vectorization in Julia
Conclusion
- Julia's a very a new language compared to C++, MATLAB, Python
- Mostly used in scientific computing, but designed to be good at many things
- JIT compiled to native code thanks to LLVM, faster than interpreted languages like Python, slower than compile-ahead-of-time languages like C++
- Although slower than C++, implements simpler syntax (looks similar to Python)
- The default compiler takes care of some optimization tasks for you. Don't need to worry about locality of reference (loop interchange)
- Multi-threading is still experimental, and it's recommended to use distributed processing or coroutines (green threads) for parallelism