Tutorial4: Data Representation / Numbering Conversion / File Permissions
Contents
- 1 Data Representation / Numbering Conversion / File Permissions
- 2 KEY CONCEPTS
- 3 INVESTIGATION 1: NUMBERING CONVERSIONS
- 4 INVESTIGATION 2: FILE PERMISSIONS
- 5 LINUX PRACTICE QUESTIONS
Data Representation / Numbering Conversion / File Permissions
Main Objectives of this Practice Tutorial
- Understand the importance of how computers store data (i.e. data representation)
- Understand the purpose of decimal, binary, octal and hexadecimal numbers
- Perform various numbering conversions between the decimal, binary, octal and hexadecimal numbering systems
by hand without the use of a computer or calculator
- Perform various numbering conversions between the decimal, binary, octal and hexadecimal numbering systems
- Identify which numbering system conversion method to use when required to perform a numbering conversion
- Understand directory and regular file permissions
- Learn how to set directory and regular file permissions with the chmod command (symbolic and octal methods)
- Learn how to use the umask command to have permissions for directories and files automatically set upon their creation
- Learn how to use the umask command to have permissions for directories and files automatically set upon their creation
Tutorial Reference Material
| Course Notes |
Numbering Conversion / File Permissions Reference |
YouTube Videos | |
| Slides:
|
Data Representation Definitions | File Permission Concepts
File Permission Commands |
Instructional Videos: |
KEY CONCEPTS
Why Study Data Representation?
Data (treated as singular, plural, or as a mass noun) is any sequence of one or more symbols given meaning by specific act(s) of interpretation.
Digital data is data that is represented using the binary number system of ones (1) and zeros (0), as opposed to analog representation.
Reference: https://en.wikipedia.org/wiki/Data_(computing)
Therefore, computers process and store information in a binary number system consisting of 0s and 1s. For many aspects of programming and networking, the details of data representation must be understood.
Reasons to Understand Data Representation:
- C Programming: Sending information over networks, files
- Web Development: Setting color codes for webpage background or text
- Allowing or Limiting Unix / Linux File Access: Setting permissions for files and directories
In terms of this course, we will learn how a simple decimal number (integer) is stored into the computer system as a binary number. We will also learn other numbering systems (octal and hexadecimal) that can be used as a "short-cut" to represent binary numbers.
Decimal / Binary / Octal / Hexadecimal Numbering Systems
Decimal Numbers
The decimal numbering system is a numbering system where each digit can be represented by numbers 0 - 9. The reason for this system may be attributed to the fact that humans were used to counting on their fingers and thumbs.
The numbering system is based on sums of the power of 10.
According to the diagram to the right, each digit moving to the left of units value is the placeholder multiplied to the power of ten. Units are ten to the power of zero (which is 1), tens are ten to the power of one, etc.
Binary Numbers
The binary numbering system is a numbering system where each digit can be represented by numbers 0 or 1. Digital computers have data-paths that can represent those 0s and 1s based on voltage levels.
The numbering system is based on sums of the power of 2.
According to the diagram to the right, each digit moving to the left of units value is the placeholder multiplied to the power of two. Units are ten to the power of zero (which is 1), then two to the power of one (which is 2), etc.
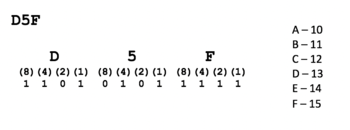
Octal / Hexadecimal Numbers
The octal and hexadecimal numbering systems are represented by values of 0 - 7 and 0 - F respectively. For hexadecimal numbers, values for 10 to 15 (which can only be represented by a single digit) use letters a to f respectively.
The numbering system is based on sums of the power of 2.
According to the diagram to the right, each digit moving to the left of units value is the placeholder multiplied to the power of two. Units are ten to the power of zero (which is 1), then two to the power of one (which is 2), etc.
Numbering Conversion Methods
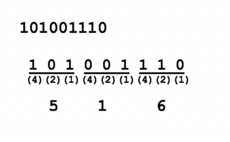
Method 1: Binary to Decimal
When converting binary numbers to decimal numbers, perform the following steps:
- Write the binary number (space between the digits).
- Starting from the right-side, draw L's moving to the left (refer to diagram on right).
- Starting on the right, multiply the number by 2 to the power of zero.
- Repeat moving to the left, but increase the power by 1 each time.
- Add up the calculations to obtain the decimal value equivalent.
NOTE: To convert other numbering system to decimal, replace the number 2
(in red in the diagram to the right) with 8 (for octal) or 16 (for hexadecimal).
Method 2: Decimal to Binary
When converting decimal numbers to binary numbers, perform the following steps:
- On the left side, write the decimal number to be converted.
- Far to the right, write the number 1 and while moving leftwards, double the number until that number is NOT greater than the decimal number to be converted (refer to the diagram).
- If you are converting to 8-bit, 32-bit, etc., enter leading zeros if those doubled numbers are greater than the decimal number.
- Moving in a rightwards direction, if the doubled number less than the decimal number, write a 1 and subtract the double number's value from the decimal number.
- If the next doubled number is greater then the remainder, then write a zero; otherwise, if the number is less than but not zero, repeat the above steps #4 and #5 until you have obtained your binary number.
Method 3: Octal to Binary / Binary to Octal
When converting decimal numbers to binary numbers, perform the following steps:
- On the left side, write the decimal number to be converted.
- Far to the right, write the number 1 and while moving leftwards, double the number until that number is NOT greater than the decimal number to be converted (refer to the diagram).
- If you are converting to 8-bit, 32-bit, etc., enter leading zeros if those doubled numbers are greater than the decimal number.
- Moving in a rightwards direction, if the doubled number less than the decimal number, write a 1 and subtract the double number's value from the decimal number.
- If the next doubled number is greater then the remainder, then write a zero; otherwise, if the number is less than but not zero, repeat the above steps #4 and #5 until you have obtained your binary number.
Method 4: Hexadecimal to Binary / Binary to Hexadecimal
When converting decimal numbers to binary numbers, perform the following steps:
- On the left side, write the decimal number to be converted.
- Far to the right, write the number 1 and while moving leftwards, double the number until that number is NOT greater than the decimal number to be converted (refer to the diagram).
- If you are converting to 8-bit, 32-bit, etc., enter leading zeros if those doubled numbers are greater than the decimal number.
- Moving in a rightwards direction, if the doubled number less than the decimal number, write a 1 and subtract the double number's value from the decimal number.
- If the next doubled number is greater then the remainder, then write a zero; otherwise, if the number is less than but not zero, repeat the above steps #4 and #5 until you have obtained your binary number.
NOTE: If you want to perform Octal to Hexadecimal or Hexadecimal to Octal numbering conversions, you can convert to binary as a bridge.
File Permissions
x
INVESTIGATION 1: NUMBERING CONVERSIONS
For this investigation, we will NOT be logged into our Matrix account, but it is recommended to have sheets of paper ready to manually perform numbering conversations.
NOTE: It is essential that you learn how to manually perform numbering conversions since you will NOT be permitted to perform quizzes, midterm, or your final exam with a computer or a calculator. Learning to quickly perform manual numbering conversions will may IT professional more productive such as setting permissions, designing computer networks, or selecting complex colors when developing webpages.
You will now get practice performing numbering conversions.
Perform the Following Steps:
- Let's convert the following 8-bit binary number 10111110 to a decimal number.
NOTE: It is extremely important to learn the correct technique to perform the
proper numbering conversion method (i.e. view the method above (drawing the L's). - Write the manual conversion on a sheet of paper.
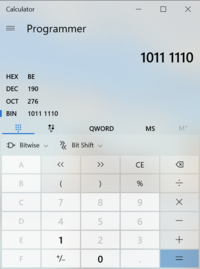
- Use a calculator to check your work. In MS Windows, you can set the calculator to Programming mode by making the selection to binary, enter the binary number 10111110 and view the decimal equivalent.
Did you get the correct answer? If not, retry the method and check to see what you did wrong. - Perform a manual conversion of the decimal number 55 to an 8-bit binary number. What method (displayed above) will you use? Use a calculator to check your work.
- Perform a manual conversion of the octal number 461 to an 8-bit binary number. What method (displayed above) will you use? Use a calculator to check your work.
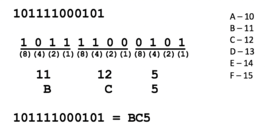
- Perform a manual conversion of the 8-bit binary number 11110001 to a hexadecimal number. What method (displayed above) will you use? Use a calculator to check your work.
- Perform a manual conversion of the hexadecimal number ABC to an 8-bit binary number. What method (displayed above) will you use? Use a calculator to check your work.
- Perform a manual conversion of the binary number 10101111 to an octal number. What method (displayed above) will you use? Use a calculator to check your work.
- Perform a manual conversion of the same binary number 10101111 to hexadecimal number. What method (displayed above) will you use? Use a calculator to check your work.
- Perform a manual conversion of the octal number 5636 to a hexadecimal number. What method (displayed above) will you use? Use a calculator to check your work.
- Perform a manual conversion of the hexadecimal number D68 to an octal number. What method (displayed above) will you use? Use a calculator to check your work.
INVESTIGATION 2: FILE PERMISSIONS
x.
LINUX PRACTICE QUESTIONS
The purpose of this section is to obtain extra practice to help with your assignment #1, quizzes, your midterm, and your final ezam.
Here is a link to the MS Word Document of ALL of the questions displayed below but with extra room to answer on the document to simulate a quiz:
https://ict.senecacollege.ca/~murray.saul/uli101/uli101_week4_practice.docx
Your instructor may take-up these questions during class. It is up to the student to attend classes in order to obtain the answers to the following questions. Your instructor will NOT provide these answers in any other form (eg. e-mail, etc).
Review Questions:
- x.
- x.
- x.
- x.
- x.
- x.
- x.
- x.
When answering Linux command questions on this side or the back side of this page, refer to the following Inverted Tree diagram. The uli101 directory is contained in your home directory. Assume that you just logged into your Matrix account. Directories are underlined.
- x
- x
- x
- x
- x
- x
- x