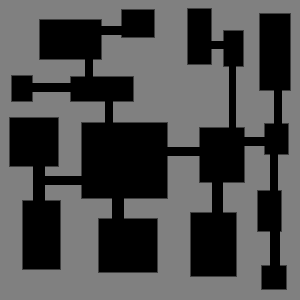Difference between revisions of "Solo Act"
(→Assignment 3) |
(→Assignment 3) |
||
| Line 73: | Line 73: | ||
[[File:njsimasroot.png|500px ]] | [[File:njsimasroot.png|500px ]] | ||
| − | |||
The first step was using modulus to set the odd value in the leaf pair equal to the greater value: | The first step was using modulus to set the odd value in the leaf pair equal to the greater value: | ||
| Line 79: | Line 78: | ||
modIndex =((ti + q) + (ti + 1) % 2) | modIndex =((ti + q) + (ti + 1) % 2) | ||
| + | I needed the number of nodes in the previous round, plus one, to later subtract from the current array index: | ||
| − | + | leafTotal ((t / 2) + 1); | |
| − | |||
| − | |||
| + | Basically 'walking backwards' | ||
The next step was making the thread index progression correspond to the root progression. | The next step was making the thread index progression correspond to the root progression. | ||
| Line 92: | Line 91: | ||
Progression = (((ti + 1) / 2) – 1) + ((ti + q) + (ti + 1) % 2) | Progression = (((ti + 1) / 2) – 1) + ((ti + q) + (ti + 1) % 2) | ||
| − | |||
Finally, I add this progression to the previous leaf total, and subtract the result from the new array index from stage 1: | Finally, I add this progression to the previous leaf total, and subtract the result from the new array index from stage 1: | ||
root = modIndex – (leafTotal + progression) | root = modIndex – (leafTotal + progression) | ||
| − | |||
Since this was all to be done by a single thread, in a single step, I condensed the formula into one line. | Since this was all to be done by a single thread, in a single step, I condensed the formula into one line. | ||
((ti + q) + ((ti + 1) % 2)) - (((((ti + 1) / 2) - 1) + ((ti + 1) % 2)) + (t / 2) + 1); | ((ti + q) + ((ti + 1) % 2)) - (((((ti + 1) / 2) - 1) + ((ti + 1) % 2)) + (t / 2) + 1); | ||
Revision as of 06:39, 16 April 2018
Contents
Solo Act
Team Members
- Nick Simas, All of the things.
Progress
Assignment 1
Profile
For assignment 1, I selected an open-source dungeonGenerator project from github.
https://github.com/DivineChili/BSP-Dungeon-Generator/
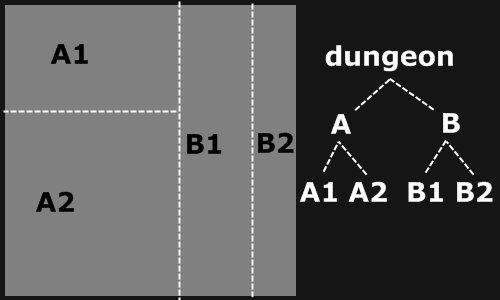
As you can see from the above images, the purpose of this program is to generate a map image for game content. The program achieves this by repetitively splitting a 2d space using a binary partition algorithm.
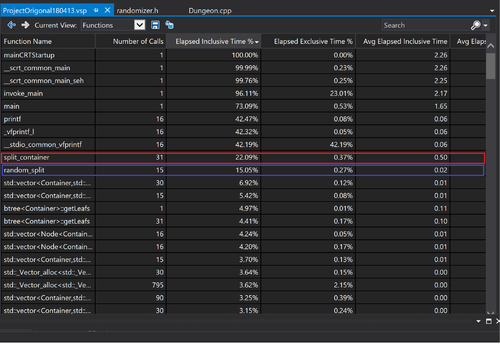
The project was written for windows, so I decided to initially profile with the built in Visual Studio profiler.
The above image shows the function inclusive time percentage. The results are 22% and 15% respectively. The only entries higher are Main and library components used for printing. This demonstrates that the majority of source code processing is occurring in these two functions. Both of them would thus are hotspots and may benefit from parallelization.
Assignment 2
Parallelize
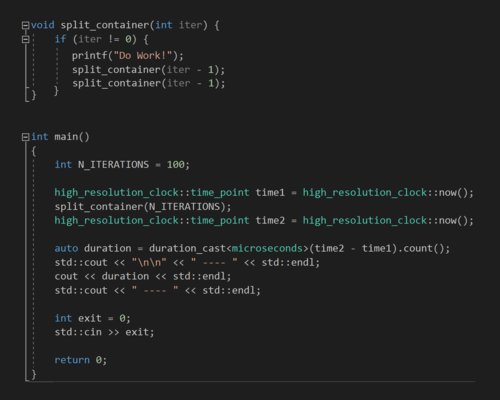
One of the immediate problems I realized with this project was that the target functions were far too large. Parallelization would require possibly three or more kernels, which was beyond the scope of this assignment. Instead I decided to focus on the bsp tree portion of the code, and decouple this portion from actual dungeon generating logic.
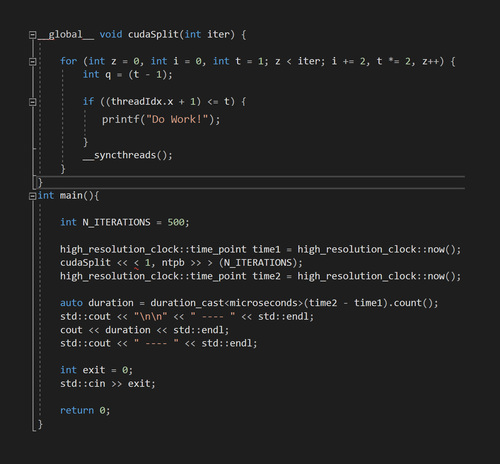
The decoupled source-code can be seen above, along with the timing logic in it's respective main function.
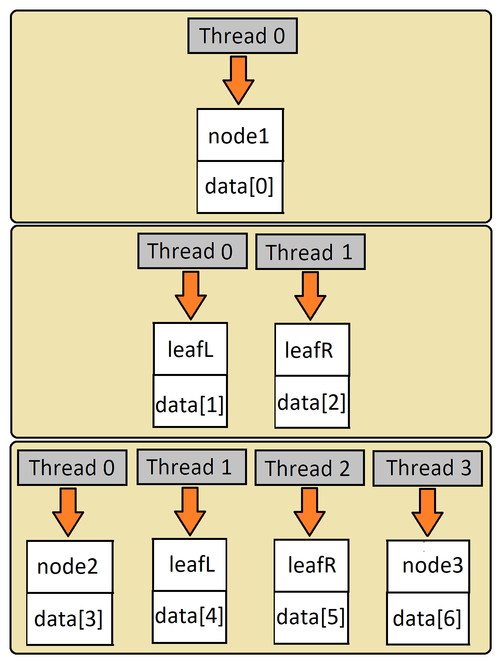
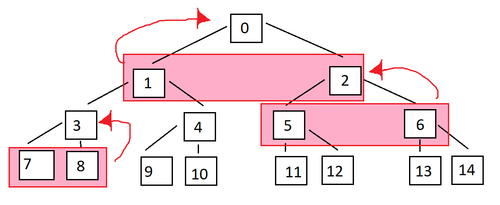
To parrellize a bsp tree required some analysis which can be seen above. The tree itself must be stored in memory according to some design. The way I decided to organize the leafs and nodes of the tree, in a linear context, can be seen below. The above image shows how the tree design corresponds to the linear arrangement in memory.
The image above reflects the design I chose with respect to the warps and thread behavior. Each warp processes a single 'round' of the tree, utilizing as many threads equivalent to the number of leaves in that 'round'.
The above image shows the kernel with the benchmarking logic in the main function. T
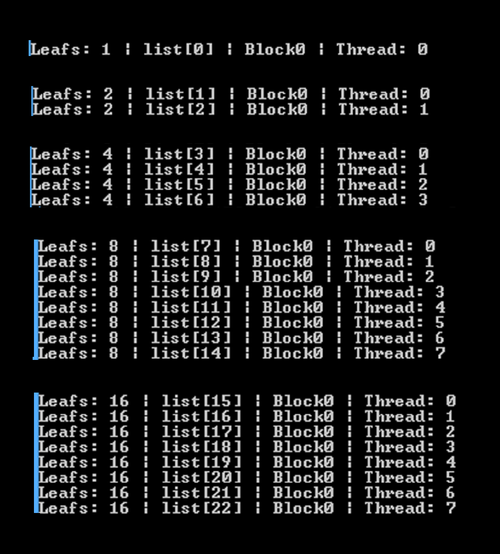
This next image shows an output example for the first five elements.
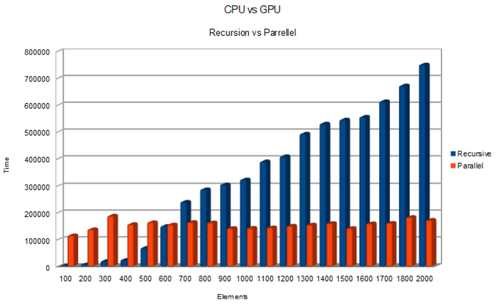
Finally, the graphs above show a comparison in performance between the first, decouple function and the previous kernel. As you can see, the original, recursive function performs faster up until the 600th element where they are equal. The parallel kernel subsequently outperforms the recursive function.
Assignment 3
From a theoretical perspective, the algorithm should benefit from shared memory access, provided there are operations being performed on the data.
To demonstrate this, I modified the kernel to perform a division on each node of the tree, storing the result in the two leaf indices.
To do this, I would need to be able to access the root node of a given leaf in a parallel way. The determinant factor would have to be the thread index. Achieving this was a bit of a math problem.
The first step was using modulus to set the odd value in the leaf pair equal to the greater value:
modIndex =((ti + q) + (ti + 1) % 2)
I needed the number of nodes in the previous round, plus one, to later subtract from the current array index:
leafTotal ((t / 2) + 1);
Basically 'walking backwards'
The next step was making the thread index progression correspond to the root progression.
For example, in round four, the thread index progression is 1, 3, 5, 7, for the greater of the leaf pair. This needed to be 0, 1, 2, 3.
To do this, I add one, divide by two, and subtract one, and then add the modulus, as in step one, to account for the lesser of the leaf pair.
Progression = (((ti + 1) / 2) – 1) + ((ti + q) + (ti + 1) % 2)
Finally, I add this progression to the previous leaf total, and subtract the result from the new array index from stage 1:
root = modIndex – (leafTotal + progression)
Since this was all to be done by a single thread, in a single step, I condensed the formula into one line.
((ti + q) + ((ti + 1) % 2)) - (((((ti + 1) / 2) - 1) + ((ti + 1) % 2)) + (t / 2) + 1);